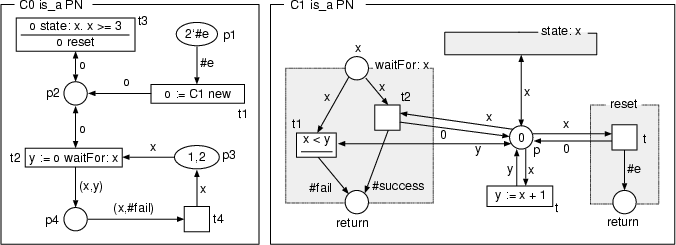
Suppose an OOPN consisting of two classes, C0 and C1. Let C0 be the initial class.

Class C0 contains only the object net. Class C1 contains its object net (place p and transition t), synchronou port state:, and methods wait: and reset.
From global poin of view, we can identify places and transitions by means of
qualified names in the form of either
The OOPN dynamics is based od high-level Petri net dynamics, but semantics of a transition is little bit modified.
A transition is fireable for some binding of variables which are present in the arc expressions of its input arcs and in its guard expression, if there are enough tokens in the input places with respect to the values of input arc expressions and if the guard expression for the given binding evaluates to true.
If a message sending (or a list of message sendings) in a guard invokes synchronous port(s), the guard is evaluated as true if the corresponding synchrounous port(s) is (are all) firable (as it was a transition) with respect to variables binding and parameter passing.
If a transition t is firable, it can be fired. Firing of a transition comprise execution of invoked synchronous ports (as it were transitions) simultaneousely with (input part of) the transition t. The transition t behaves according to its action.
Transition actions correspond to message sendings.
Without any respect to the concrete syntax, suppose transitions
actions in the form
![]() where y is a
variable, xi is a term, and msg is a message selector. The object
identified by x0 is the receiver of the message and objects xi are
message parameters. The way how a transition will be performed depends on the
class of the receiver, i.e. on the class of the object x0:
where y is a
variable, xi is a term, and msg is a message selector. The object
identified by x0 is the receiver of the message and objects xi are
message parameters. The way how a transition will be performed depends on the
class of the receiver, i.e. on the class of the object x0:
An OOPN evolution begins by an automatic creation of the so called primary object which is an instance of the primary class. This object contains an instance of the particular object net which is initialized by the initial marking. All OOPN dynamics is then given by performing transitions in running net instances which can also influence the set of existing objects and net instances. If we neglect the case of non-atomic methods of primitive objects which are not taken into account in the formal OOPN definition, all evolution steps have the form of atomic events. These events are connected to transitions in the following way:
An implicit part of every event occurrence is the so called garbage collecting, i.e. shredding all net instances as well as objects which are not transitively accessible from the primary object.
A state of the system corresponding to a running OOPN can be defined as a set of objects composed of running net instances, whose states are given by their markings. A marking m of a net instance (id,m), where id is an unambiguous identification of the net instance, specifies for every place a multiset of tokens referring to objects, and for every transition a set of invocations.
A state of a running OOPN can be specified by following table:
| identifiers of currently running objects, identifiers of net instances contained in objects | |
| OOPN structure - classes containing nets comprising places and transitions | marking of
places and transitions in net instances |
The initial state of our OOPN is defined by the state of the initial object (instance of the initial class). It contains initial marking of C0's object net. Let the initail object as well as its object net instance have name id0The initial state (named S0) of our OOPN can be specified by following table:
| id0 | |||
| id0 | |||
| C0 | object | p1 | 2`#e |
| p2 | empty | ||
| p3 | 1, 2 | ||
| p4 | empty | ||
| t1 | empty | ||
| t2 | empty | ||
| t3 | empty | ||
| C1 | object | p | |
| t | |||
| wait: | x | ||
| return | |||
| t1 | |||
| t2 | |||
| reset | return | ||
| t |
[ It is recommended to open a new browser window on this page to show the OOPN structure (the picture above) simultaneously with tables depicting the OOPN states. ]
In the state S0, the transition C0::t1 firable in net instance id0 is n-firable, i.e. it is able to create a new object (it is specified by the transition action o := C1 new). The transition does not contain any input variable, thus the variables binding is empty. The event corresponding to n-firing of this transition can be specified as
[ N, id0, C0::t1, () >
This event occurrence changes the system state following way:
| id0 | id1 | |||
| id0 | id1 | |||
| C0 | object | p1 | #e | |
| p2 | id1 | |||
| p3 | 1, 2 | |||
| p4 | empty | |||
| t1 | empty | |||
| t2 | empty | |||
| t3 | empty | |||
| C1 | object | p | 0 | |
| t | empty | |||
| wait: | x | |||
| return | ||||
| t1 | ||||
| t2 | ||||
| reset | return | |||
| t |
In this tate, the following events are executable:
Execution of f-event
[ F, id0, C0::t2, (x=1, o=id1) >
leads to the OOPN state change:
| id0 | id1 | ||||
| id0 | id1 | id2 | |||
| C0 | object | p1 | #e | ||
| p2 | id1 | ||||
| p3 | 2 | ||||
| p4 | empty | ||||
| t1 | empty | ||||
| t2 | (id2, x=1, o=id1) | ||||
| t3 | empty | ||||
| C1 | object | p | 0 | ||
| t | empty | ||||
| wait: | x | 1 | |||
| return | empty | ||||
| t1 | empty | ||||
| t2 | empty | ||||
| reset | return | ||||
| t | |||||
In this state, the following events are executable:
Execution of event
[ F, id0, C0::t2, (x=2, o=id1) >
leads to creation of a new instance of the method net C1::wait: in object id1. This instance will be named id3. The resulting state can be described by following table:
| id0 | id1 | |||||
| id0 | id1 | id2 | id3 | |||
| C0 | object | p1 | #e | |||
| p2 | id1 | |||||
| p3 | empty | |||||
| p4 | empty | |||||
| t1 | empty | |||||
| t2 | (id2, x=1, o=id1), (id3, x=2, o=id1) | |||||
| t3 | empty | |||||
| C1 | object | p | 0 | |||
| t | empty | |||||
| wait: | x | 1 | 2 | |||
| return | empty | empty | ||||
| t1 | empty | empty | ||||
| t2 | empty | empty | ||||
| reset | return | |||||
| t | ||||||
In this state, the following events are executable:
Execution of event
[ A, id1, C1::t, (x=0) >
means classical atomic execution of C1::t in net instance id1. The resulting state can be described by following table:
| id0 | id1 | |||||
| id0 | id1 | id2 | id3 | |||
| C0 | object | p1 | #e | |||
| p2 | id1 | |||||
| p3 | empty | |||||
| p4 | empty | |||||
| t1 | empty | |||||
| t2 | (id2, x=1, o=id1), (id3, x=2, o=id1) | |||||
| t3 | empty | |||||
| C1 | object | p | 1 | |||
| t | empty | |||||
| wait: | x | 1 | 2 | |||
| return | empty | empty | ||||
| t1 | empty | empty | ||||
| t2 | empty | empty | ||||
| reset | return | |||||
| t | ||||||
In this state, the following events are executable:
Execution of a-event
[ A, id2, C1::wait:::t2, (x=1) >
leads to new state:
| id0 | id1 | |||||
| id0 | id1 | id2 | id3 | |||
| C0 | object | p1 | #e | |||
| p2 | id1 | |||||
| p3 | empty | |||||
| p4 | empty | |||||
| t1 | empty | |||||
| t2 | (id2, x=1, o=id1), (id3, x=2, o=id1) | |||||
| t3 | empty | |||||
| C1 | object | p | 0 | |||
| t | empty | |||||
| wait: | x | empty | 2 | |||
| return | #success | empty | ||||
| t1 | empty | empty | ||||
| t2 | empty | empty | ||||
| reset | return | |||||
| t | ||||||
In this state, the following events are executable:
The place return in the instance id2 of the net C1::wait was in previous step marked by symbol #success. It means that the method is able to return its result to the transition t2 in the instance id2 of the net C0. This transition is j-executable for variables binding (x=1, o=id1), because its matking contain item (id2, x=1, o=id1) and place return in id2 has nonempty marking. Execution of j-event
[ J, id0, C0::t2, (x=1, o=id1, y=#success) >
leads to deletion of net instance id2 and execution of output part of t2 in net instance id0. The resulting state can be described by following table:
| id0 | id1 | ||||
| id0 | id1 | id3 | |||
| C0 | object | p1 | #e | ||
| p2 | id1 | ||||
| p3 | empty | ||||
| p4 | (1, #success) | ||||
| t1 | empty | ||||
| t2 | (id3, x=2, o=id1) | ||||
| t3 | empty | ||||
| C1 | object | p | 0 | ||
| t | empty | ||||
| wait: | x | 2 | |||
| return | empty | ||||
| t1 | empty | ||||
| t2 | empty | ||||
| reset | return | ||||
| t | |||||
And so on ..........