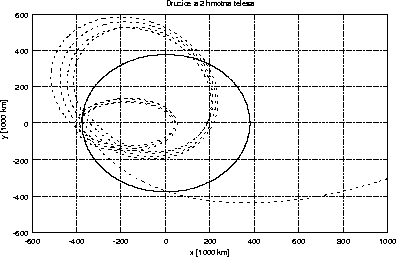
Figure: Družice v gravitačním poli
Uvažujme systém Země-Měsíc a družici, která má vhodně zvolenou počáteční pozici a rychlost. Takový systém můžeme popsat takto:
// druzice.cc -- model Země--Měsíc--družice
#include "simlib.h"
#include "simlib3D.h"
typedef Value3D Position, Speed, Force;
const double gravity_constant = 6.67e-11; // gravitační konstanta
const double m0 = 1000; // hmotnost družice
const double m1 = 5.983e24; // hmotnost Země
const double m2 = 7.374e22; // hmotnost Měsíce
const Position p0(36.0e6, 0, 0); // poloha družice
const Position p2(384.405e6, 0, 0); // poloha Měsíce
const Speed v0(0, 4.5e3, 0); // počáteční rychlost družice
const Speed v2(0, 1022.6, 0); // oběžná rychlost Měsíce
Constant3D Zero(0,0,0); // pomocný objekt
struct MassPoint {
double m; // hmotnost
Expression3D inforce; // vstupní síla
Integrator3D v; // rychlost
Integrator3D p; // pozice
MassPoint(const double mass, Position p0, Speed v0=Speed(0,0,0)) :
m(mass),
inforce(Zero),
v(inforce/m, v0),
p(v,p0) {}
void SetInput(Input3D i) { inforce.SetInput(i); }
};
struct MyWorld { // digitální svět
enum { MAX=10 };
MassPoint *m[MAX];
unsigned n;
MyWorld();
};
MyWorld *w; // vznikne až později :-)
// gravitační síla pusobící na hmotný bod p
class GravityForce : public aContiBlock3D {
MassPoint *p;
MyWorld *w;
public:
GravityForce(MassPoint *_p, MyWorld *_w) : p(_p), w(_w) {}
Force Value() {
Force f(0,0,0); // gravitační síla
for(int i=0; i < w->n; i++) {
MassPoint *m = w->m[i];
if (m == p) continue;
Value3D distance = m->p.Value() - p->p.Value();
double d = abs(distance); // vzdálenost
f = f + (distance * gravity_constant * p->m * m->m / (d*d*d)) ;
}
return f; // součet všech gravitačních sil
}
};
typedef MassPoint Planet, Satelite; // pohyblivé planety
MyWorld::MyWorld() { // --- vytvoříme digitální svět
n=0;
m[n++] = new Planet(m1,Position(0,0,0),Speed(0,0,0));
m[n++] = new Planet(m2,p2,v2);
m[n++] = new Satelite(m0,p0,v0);
for(int i=0; i<n; i++) // --- zapneme silové působení
m[i]->SetInput(new GravityForce(m[i],this));
}
Třída MassPoint definuje model hmotného bodu. Vstupem tohoto modelu je
síla, která způsobí jeho pohyb. Protože model vytváříme postupně, je
implicitně tato síla nulová a nastaví se až po vytvoření všech hmotných bodů v
systému (viz konstruktor třídy MyWorld). Celý model je tvořen třídou
MyWorld,
která obsahuje seznam všech hmotných bodů.
Třída GravityForce modeluje gravitační sílu a je pro každý hmotný bod
definována jako součet všech gravitačních sil působících na hmotný bod.
Gravitační síla se počítá se podle gravitačního zákona.
Výsledná dráha družice a Měsíce je uvedena na obrázku 8.

Figure: Družice v gravitačním poli